Uit opiniepeilingen wordt maar al te vaak nieuws gefabriceerd dat, statistisch gezien, helemaal niet klopt, meent politicoloog Tom Louwerse.
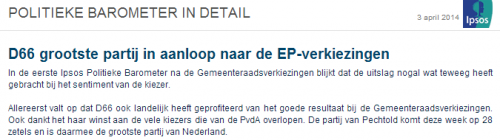
Dan toch maar weer een stukje over peilingen. Leuker kunnen we het niet maken, wel beter. Steen des aanstoots was deze keer de Politieke Barometer van Ipsos:
D66 was dus de grootste partij van Nederland met 28 zetels volgens de peiler. Ipsos is de enige peiler die ook netjes de percentages presenteert: 18,5% van de respondenten gaf aan nu D66 te stemmen. Daarna volgt de VVD met 17,2% (26 zetels).
Maar wacht, denkt de oplettende lezer nu, dat verschil van 1,3% is helemaal niet zo groot. Weten we wel zeker op basis van een onderzoek onder 1004 mensen dat D66 onder de gehele kiesgerechtigde bevolking de grootste is?
Ipsos is de beroerdste niet en geeft zelf aan met welke foutmarges de peiling te maken heeft:
Bij de steekproeven die per peiling worden gebruikt zijn die marges gemiddeld bij de kleine partijen +/- 1% en bij de grootste partijen +/- 2.5%.
Die 2,5% is toch een stuk meer dan het verschil tussen D66 en de VVD. Nu gaat die marge hier niet helemaal op, want strikt genomen moeten we kijken naar de marge van het verschil tussen D66 en VVD. Voor een aselecte steekproef valt die marge voor zo’n verschil eenvoudig uit te rekenen. Ook op die manier blijkt dat we op basis van deze ene peiling helemaal niet kunnen concluderen dat D66 ‘de grootste partij van Nederland is’.
Disclaimers zijn leuk, maar je moet ze natuurlijk ook zelf lezen. Dit is niet de eerste keer dat er in de kop van een nieuwsbericht een claim staat die door de disclaimer onderuit wordt gehaald. Vaak zijn het media die de fout ingaan, maar soms proberen peilers hun resultaten ook stelliger voor te doen dan ze zijn.
Nu zeggen sommige journalisten wel eens: ‘maar wij zeggen dat D66 in de peiling groter is dan de VVD, en dat klopt feitelijk.’ Juist. Maar het is ook irrelevant. Wat doet het er toe wat tante Sjaan uit Bovenkarspel en Ali uit Rotterdam en 1002 respondenten in een peiling zeggen? Helemaal niets. Een peiling is interessant wanneer deze iets zegt over het hele electoraat (of een groep daarbinnen).
Nu kunnen we ons daar ontzettend boos over maken – en dat doe ik dan ook graag – maar misschien werkt een hulpmiddel beter. Met deze tool kan je, na het invullen van het aantal respondenten in de steekproef en de zetelaantallen voor de twee partijen, gemakkelijk kijken of het verschil tussen die twee partijen statistisch significant is. Is dat het geval, dan kun je op basis van de peiling uitspraken doen over alle kiezers. Zo niet, kies dan beter een andere kop voor je nieuwsbericht.
Dit artikel verscheen eerder op Stuk Rood Vlees.

Reacties (8)
Als we toch spijkers op laag water zoeken …
“statistisch gezien, helemaal niet klopt”
moet zijn “statistisch gezien, niet helemaal klopt”
“2,5% is toch een stuk meer dan het verschil tussen D66 en VVD”
moet zijn 5% (2,5% voor elk)
Dit is wel een grappige tool, je moet er eigenlijk nog wel even bij zeggen welke assumpties je maakt over de verdeling.
Anders is die niet compleet, want zonder een uitspraak over de spreiding te doen is het niet mogelijk om te zien hoe je uit alleen het aantal observaties tot de standaardfout komt.
@2: Het is een multi-nomiale verdeling dus de spreiding volgt uit de p’s.
@3: De steekproeven zijn waarschijnlijk niet getrokken volgens een perfect gerandomiseerd model (i.e. dat elke stemmer evenveel kans heeft om in de steekproef opgenomen te worden). In het bijzonder zullen de onderzoeksbureaus meestal corrigeren voor onder- of bovenrepresentatie van bepaalde bevolkingsgroepen (mannen, hoogopgeleiden, of wat dan ook). Zodra dat gebeurt kun je de gewone multi-nomiale verdeling eigenlijk niet meer gebruiken om de steekproeffout mee te bepalen (het blijft meestal wel een goede benadering).
Daarom moet er dus bij de tool gezegd worden dat de aanname van multinomiale verdeling gedaan is (als dat zo is).
@2 @3 @4: Mijn toelichting op dit punt, wel gepubliceerd op Stuk Rood Vlees, heeft men hier weggelaten:
“Naschrift: je kunt je afvragen of de formules op basis van aselecte steekproeven wel van toepassing zijn bij internetpeilingen (waarbij ook nog allerlei wegingsprocedures plaatsvinden). Feit is dat de door Ipsos gepresenteerde foutmarges vergelijkbaar zijn met die van een aselecte steekproef, dus nemen we die als leidraad. In het model van de Peilingwijzer houd ik er rekening mee dat de werkelijke foutmarges kleiner of groter kunnen zijn dan bij een aselecte steekproef. Dit verschilt per partij: soms zijn de marges kleiner, vooral bij stabiele partijen als de SGP, soms net wat groter.”
http://stukroodvlees.nl/peilingen/disclaimers-zijn-niet-voor-de-sier/
@1: Heb je het stuk goed gelezen?
“Nu gaat die marge hier niet helemaal op, want strikt genomen moeten we kijken naar de marge van het verschil tussen D66 en VVD.”
De foutmarge van het verschil is *niet* 2 maal 2,5%, maar iets kleiner. Daarvoor heb ik nu juist de link naar de tool toegevoegd.
Je kan toch wel zeggen (als ik het goed berekend heb tenminste): 75% kans dat D66 de grootste partij is. Dat is het niveau waarop het wel significant is.
@7: Dat zou een onjuiste interpretatie van de significantiewaarde (p-waarde) zijn. De juiste interpretatie is vrij gecompliceerd: als er in de populatie geen verschil tussen D66 en VVD is (de nulhypothese), is de kans dat we (bij het herhaaldelijk uitvoeren van het steekproefonderzoek) een verschil krijgen dat minstens zo groot is als wat we hier vinden 25%. Dus in één op de vier replicaties van ons onderzoek zouden we onterecht concluderen dat D66 groter is dan de VVD.
Als je de meer intuïtieve interpretatie wilt gebruiken (“75% kans dat D66 de grootste is”) moet je Bayesiaanse statistiek gebruiken.