Kunst op Zondag | Koepelbouw

Het plaatje hierboven toont de noordelijke koepel van de Vrijdagsmoskee in Isfahan. Een inscriptie vertelt dat het gewelf is gebouwd door een voorname hoveling, Taj al-Molk, in het jaar dat wij 1088 noemen. De constructie heeft een doorsnede van ongeveer negen meter: niet heel groot, maar toch noemde de architectuurhistoricus Arthur Pope het in zijn boek Persian Architecture “perhaps the most perfect dome known”.

Hij had het ook over “the perfection of a sonnet”, en hoewel ik die vergelijking niet zo goed begrijp, is wel duidelijk dat hij onder de indruk was van deze koepel. Daar is ook alle reden toe, want dit gewelf kan eigenlijk niet bestaan. Dat vergt wat uitleg.

Rond en vierkant

Koepels hebben de onhebbelijke eigenschap rond te zijn. Als je de koepel op de grond zet, levert dat geen problemen op, denk maar aan een iglo. Het wordt anders als je de koepel bovenop een gebouw wil zetten. De Romeinse architect die het Pantheon bouwde, ontweek het probleem door onder het gewelf een eveneens rond gebouw te plaatsen, maar dit is vaak geen praktische vorm. Bouw maar eens een kast voor een ronde kamer.

Kortom: hoe plaatsen we een ronde koepel op een vierkante ruimte, een iglo bovenop een kubus? De simpelste oplossing is dat je in het dak van de kubus een rond gat maakt en daaromheen de koepel bouwt. Dat is ook wel eens gedaan, zoals in het charmante vijfde-eeuwse jachtpaleisje te Sarvestan in het zuiden van Iran. Er kleeft echter een heel groot nadeel aan deze constructiewijze: het gewicht van de koepel rust op slechts vier plaatsen, namelijk daar waar de onderrand van de koepel rust op de verticale muren. De koepel kan daarom nooit al te groot worden, omdat het gewicht de muren uit elkaar duwt.

Sultaniye

Het zou al makkelijker zijn als je een achthoekig gebouw hebt: dan heb je (anders dan in een Pantheon-achtig gebouw) in elk geval rechte muren om een kast tegenaan te zetten. Bovendien wordt in een achthoekig gebouw de druk van de koepel over het dubbele aantal punten verdeeld. De Rotskoepel in Jeruzalem is het bekendste voorbeeld; een ander voorbeeld is het kolossale mausoleum in Sultaniye, in noordwestelijk Iran. Toevallig heeft mijn zus ooit een foto genomen waarop is te zien hoe ik, barbaar, sta te telefoneren met de rug naar dat schitterende veertiende-eeuwse grafmonument.

Mausoleum in Multan

Maar ook een achthoekig gebouw als basis voor een koepel is nog verre van volmaakt. Een van de nadelen is goed te zien op de foto hierboven: het mausoleum van shah Rukn-e Alam uit Multan in Pakistan, ruwweg even oud als de koepel van Sultaniye. Weliswaar is de druk nu dus over acht in plaats van vier punten verdeeld, maar je hebt nog steeds zware steunberen nodig om te voorkomen dat het gewicht van de koepel de dragende muren uit elkaar duwt en het gebouw doet instorten.

Trompen

Achthoekige gebouwen zijn van de Late Oudheid tot het einde van de Middeleeuwen populair geweest, maar verdwenen weer toen bleek dat het toch mogelijk was een koepel op een vierkante ruimte te plaatsen. Het achthoekige plattegrond van de structuur onder de koepel was als oplossing niet langer noodzakelijk.

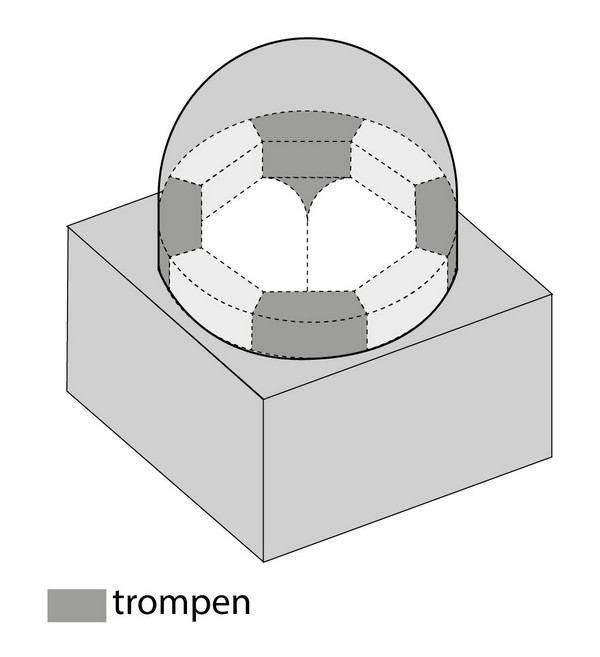
Een koepel rustend op vier muren en vier trompen (met dank aan Kees Huyser)

De nieuwe oplossing was dat men een achthoekige overgangszone construeerde tussen de kubus en de koepel. Zie het tekeningetje hierboven. Een van de oudste mij bekende voorbeelden komt, alweer, uit Iran en is te zien op de foto hieronder: het paleis van koning Ardašir I (r.224-241) in Firuzabad.

Firuzabad

Onderaan op de foto zie je een vierkante ruimte, die zich uitstrekt tot aan de onderste van de twee lijsten; daarboven zie je (met enige moeite) dat de linker- en de rechterhoek zijn afgesneden; en daarboven ligt een ronde lijst, waarop de koepel rust. Het is nog wat onbeholpen. De zone tussen de twee lijsten is niet echt mooi, en was in de Oudheid dan ook versierd met stucwerk. Maar het voordeel van de constructie is dat de druk van de koepel nu gelijkmatiger over de vier onderliggende muren werd verdeeld.

De afgesneden hoeken staan bekend als “trompen” en in een iets verder uitgewerkte vorm als “pendentieven”. Wie in West-Europa een barokkerk bezoekt, zal opvallen dat ze vaak beschilderd zijn met de portretten van de vier evangelisten.

Veelvouden van twee

Maar waarom zou je je beperken tot het afsnijden van maar vier hoeken en het scheppen van een achthoek? We kunnen toch ook de hoeken van de achthoek afsnijden en een zestienhoek maken? Of een tweeëndertighoek? Dat levert een nóg regelmatigere verdeling van de druk op.

En nu komen we in Isfahan, waar van 1072 tot 1092 koning Malik Shah regeerde. Zijn vizier Nizam al-Molk (“orde van het land”) bouwde in 1086-1087 de zuidelijke koepel van de Vrijdagsmoskee. Het was een ambitieus project, want van onder naar boven is er sprake van een vierhoekige ruimte die via een achthoek, een zestienhoek en een tweeëndertighoek overgaat in een mooie ronde koepel.

De rivaal van Nizam al-Molk, de al genoemde hoveling Taj al-Molk (“kroon van het land”), kon dat niet op zich laten zitten en bouwde de noordelijke koepel van de Vrijdagsmoskee. Kijk nu nog even naar de foto hierboven (of klik hier). In de hoeken van de foto ziet u delen van de vier trompen en daarboven ligt de zestienhoek waarop het gewelf rust. Tot zover is er niets aan de hand, maar kijk nu even naar de decoratie: dat is een vijfpuntige ster. De punten vormen een regelmatige vijfhoek.

En daar wringt het. Vier, acht, zestien en tweeëndertig zijn machten van twee (je kunt ze schrijven als 2ⁿ). Ze zijn niet deelbaar door vijf, en dat zal je ook niet lukken met 64, 128, 256, 512, 1024, 2048… Nooit eindigt het getal op een vijf of een nul. Verschillende mensen hebben daarom de vraag gesteld hoe de makers van deze koepel erin zijn geslaagd een regelmatige vijfhoek te construeren binnen een zestienhoek. Dat kun je, simpel gezegd, niet met een liniaal en een passer.

Omar Khayyam?

De enige die rond 1088 de wiskundige kennis bezat om het probleem aan te pakken, was Omar Khayyam, die derdegraadsvergelijkingen kon oplossen. Veel reisgidsen vertellen daarom dat de geleerde dichter-filosoof-astronoom-wiskundige ook nog architect was, waarbij een belangrijk argument is dat er een romantisch verhaal bestaat dat hij al sinds zijn jeugd bevriend was met zowel vizier Nizam al-Molk als Hasan-e Sabah, de grondlegger van de religieuze orde der Assassijnen. U kent die laatste misschien als de “oude man van de bergen” uit de verhalen van Marco Polo.

Alleen, de vriendschap tussen deze drie mannen is vrijwel zeker fictief. Om te beginnen kunnen ze om chronologische redenen onmogelijk al sinds hun jeugd bevriend zijn geweest: Nizam al-Molk was dertig jaar ouder dan Omar Khayyam en Hasan-e Sabah. Bovendien is het verhaal pas twee eeuwen later opgetekend door een encyclopedist uit Hamadan, Rashid ad-Din Fadhlallah. Twee eeuwen is veel tijd, genoeg om een volksverhaal te laten ontstaan waarin drie van Irans superhelden – de geleerde, de bestuurder en de religieuze leider – met elkaar in verband werden gebracht.

Er is nog een ander bezwaar. Zelfs als Omar Khayyam bevriend was met Nizam al-Molk, dan is het toch wel raar dat hij uitgerekend diens aartsvijand Taj al-Molk hielp bij het construeren van een koepel die het bouwwerk van Nizam al-Molk in de schaduw stelde.

Ik denk dat er eigenlijk gewoon geen probleem is. De vraag hoe je binnen een zestienhoek een vijfhoek construeert, is intellectueel interessant, maar we hebben niet te maken met een intellectueel maar een architectonisch probleem. Ik denk dat de ontwerper heel simpel de 360⁰ van de cirkel door vijf heeft gedeeld en wist dat zijn vijfhoek om de 72⁰ een punt moest hebben. Het is jammer, want het zou leuk zijn geweest als Omar Khayyam een bijdrage had geleverd aan ’s werelds perfectst-bekende koepel, mais on n’a pas besoin de cette hypothèse.