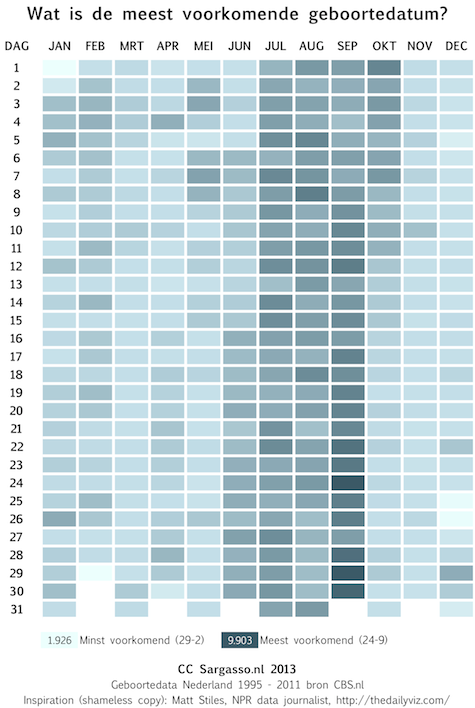
DATA - In Nederland komen verhoudingsgewijs de meeste kinderen in september ter wereld. Ze worden dus verwekt in de donkere decembermaand. 24 september is de meest voorkomende dag en 29 februari uiteraard de minst voorkomende.
Als je alle geboortes van de periode 1995 tot 2011 neemt, wat leert ons dat dan?
Dat op 24 september de meeste kinderfeestjes plaatsvinden (9903). En dat er dus heel veel grote mensen seks hadden rond 18 december 1 januari. Op de tweede plaats staat 29 september met 9899 geboortes. Die moeten dan op kerstavond verwekt zijn Dat waren goede voornemens.
De minst voorkomende geboortedag is uiteraard 29 februari met slechts 1926. Maar als we die buiten beschouwing laten vanwege zijn bijzondere karakter, is 1 januari de laagste met 6565 geboortes. Op 18 oktober, de datum vandaag, werden sinds 1995 8867 kinderen geboren.
Het gemiddelde per dag is ongeveer 8925. Dat is over zeventien jaar genomen. Per dag per jaar is het dan 525 geboortes.
Het valt sowieso op dat vaste feestdagen allemaal laag scoren. Koninginnedag met 7953, 5 december met 7639, 25 december met 6806 en 26 december met 6709. Ongeveer drie dagen later is er dan weer een klein geboortegolfje. Oftewel, het uitstellen van een geboorte lijkt mogelijk te zijn.
De minst populaire maand is december met gemiddeld 499 verjaardagen per dag (in één jaar). De meest populaire maand is september met gemiddeld 557 verjaardagen per dag.
Waar we nu nieuwsgierig naar zijn is of dit ook in het verleden zo was. We zijn nog op zoek naar de gegevens van ver voor 1995 om een mooie vergelijking te kunnen maken tussen verschillende tijdvakken. Tips of hele datasets zijn welkom.
Overigens is deze post 100% geïnspireerd door het fraaie voorbeeld van Matt Stiles.
Dank ook aan Jaap Meijers, Ionica Smeets, Rob Nijman, Numrush, Lex Slaghuis en Conrad Berghoef voor het helpen zoeken van de data en Steven Lenos voor de tip.
Hier de spreadsheet met resultaten in Excel-formaat. En ja, bovenstaand plaatje is helemaal in Excel tot stand gekomen.

Reacties (22)
Mooi, en dan nu nog de dooien. Welke dag moeten we vrezen?
Leuke cijfers, Steeph!
De verklaring lijkt mij dat er op feestdagen minder bezetting is in de ziekenhuizen. Ze doen dan geen geplande inleidingen en sectio’s.
29 februari is makkelijk te corrigeren door het getal te vermenigvuldigen met 4. Dan kom je op 7704, nog steeds laag.
Rond kerst en oud & nieuw heeft menigeen vrij, is het koud en donker. Het is ook nog feesttijd en gezelligheid met alcohol enzovoorts. Dus alle reden om even lekker dicht tegen elkaar aan te kruipen.
@3: Dat kan. Maar dan is de correcte berekening delen door 4 (aantal schrikkeljaren van toepassing) en vermenigvuldigen met 17 (aantal jaren in de meting). Dan kom je uit op 8186. Ook nog onder het gemiddelde.
@2: zijn er op zondagen ook minder geboorten is dan de vraag
@5: Ja. Had geen zin om die zelf te maken. Hier een eerder onderzoek:
http://www.cbs.nl/nl-NL/menu/themas/bevolking/publicaties/artikelen/archief/2004/2004-1423-wm.htm
@4 Het is ook significant minder. Als je uitgaat van poisson gebeurtenissen is de variantie 44 op 1926. Je verwacht er 2100. Het lijkt er op dat er een kleine neiging is deze geboortedatum (‘verjaardag’) te vermijden, mischien is het dus mogelijk een uurtje te sjoemelen met het geboortetijdstip? Langs die lijn lijkt er ook een kleine neiging te zijn de 13e te vermijden.
@7: Bij inleidingen en geplande sectio’s doen ze er idd vaak niet al te moeilijk over om het een dagje later te doen, dus dat effect zal daar ook spelen.
Het beeld is hetzelfde als die versie van Stiles voor de USA. Het lijkt gerechtvaardigd dat dit beeld (kort na 21 september september geboorte maximum) voor het hele Noordelijk halfrond geldt.
Ik verwacht dan, voor het zuidelijk halfrond, een piek kort na 21 maart. Voor het gebied tussen de keerkringen verwacht ik een evenwichtige spreiding.
Anders gezegd : het is een verdeling die afhankelijk is van de geografische breedte.
@3: Deze set bestaat uit 17 jaar, waarin er 4 schrikkeljaren waren. Je moet dus iets anders corrigeren: (1926/4)*17 = 8185.5. Nog steeds 10% onder het gemiddelde, maar wel een stukje minder erg.
Hier uit volgt:
Het “kindeke-in-de-kribbe-gedoe” is mede oorzaak van de overbevolking ;-)
Deze uitvoering is ook mooi
http://vizwiz.blogspot.nl/2012/05/how-common-is-your-birthday-find-out.html
Ga ik binnenkort maar eens proberen.
@9: Uit een vergelijking met het zuidelijk halfrond kan inderdaad duidelijk worden of december hier een populaire vrijmaand is vanwege de duisternis of door de vrije dagen.
Het schema ziet er aangenaam uit, maar gewoon in een grafiekje zetten is ook leerzaam. Met de datum op de x-as en aantal geboortes en verwekkingen (286 dagen eerder) op de y-as. Als je de y-as tussen de 8.000 en 10.000 zet, zie je dat er in het nieuwe jaar eerst maar eens de goede voornemens moeten worden behaald voordat men aan verwekkingen begint. Als na de zomervakantie voldoende vertrouwen is opgebouwd dat men de komende winter overleeft (of zo), schiet het aantal verwekkingen naar boven, met als uitschieter de kerstperiode.
Maar zet je de y-as gewoon van 0 tot 10.000, dan leert het grafiekje dat wanneer je van een 20-daags zwevend gemiddelde uitgaat (redelijk gezien de variatie in draagtijd) het aantal najaarsverwekkingen slechts 4% hoger is dan het gemiddelde en de kerstverwekking 8%. En het februaridal is ook slechts 4% lager tov het gemiddelde. Significante verschillen, maar zon- en feestdagen hebben dus meer invloed op de planning van verloskundigen.
Afijn, een grafiekplaatje was dus verhelderend geweest. Plus de vraag: waar wil je op sturen met deze data? Of is het gewoon data-vermaak?
@13: Ja, ik verwacht een biologische reden voor zo een concentratie van geboortes. Waarbij er door onze medische en technologische -licht/lampen – cultuur natuurlijk wat verschuivingen plaats zijn gaan vinden waardoor de verdeling breder is geworden.
Vind niemand anders het vreemd dat 18 december en kerstavond (23/24 december) als verwekkingsdata genoemd worden? Ik zou juist een andere analyse maken aan de hand van een andere aanname: 26 en 31 december zijn de ‘verwekkingsdagen’ en de aanname van het aantal zwangerschapsdagen (280) is met 5 overschat.
De verjaardagen van mijn familie, de meesten nu dood, lagen in januari februari.
1 april is altijd een grap geweest, of we nu over de hele maand april anders moeten gaan denken ?
@steeph: het aardige is dat je dat effect ook in andere datasets ziet waar je met geboortedata werkt (duh, natuurlijk). Maar het is wel aardig om te zien, en het is voor veel mensen even wennen om te realizeren dat dat patroon er is.
Plus de vraag: waar wil je op sturen met deze data? Of is het gewoon data-vermaak?
Uiteindelijk is geen enkele dataset of visualisatie ‘nuttig’. Eat that.
@16: Goed punt. Ik ging even te snel van de 40 weken uit. Maar dat is vanaf de laatste menstruatie (gemiddeld). Zwangerschap duurt gemiddeld 38 weken. Dat is 266 dagen. Dus tussen 1 en 6 januari :-)
Volgens dit onderzoek 268 dagen (en dus niet 286 zoals ik eerder typte, dat gold blijkbaar alleen voor mijn eigen kinderen). http://www.ad.nl/ad/nl/1003/You/article/detail/3488417/2013/08/07/Gemiddelde-zwangerschap-duurt-maar-268-in-plaats-van-280-dagen.dhtml
Die verklaring van #20 is ook meteen een stuk logischer; als je planned om zwanger te worden dan doe je dat natuurlijk NA de met alcohol overladen feestjes van eind december. Ook de piek in juli en augustus is eenvoudig te verklaren door simpele planning; bevallen in de vakantie cq een met zwangerschapsverlof verlengde vakantie is natuurlijk hartstikke fijn, evenals voor de bevalling nog even relaxt op vakantie gaan (of de kinderkamer afmaken:p).
Dus volgens mij zien we in die piek niet zoveel feestjesbabies of babies die alleen maar verwekt zijn omdat papa en mama “eindelijk” weer eens sex hadden, geinspireerd door de donkere dagen. Dan zou de hele piek bestaan uit “ongelukjes”. En daar geloof ik niks van. De piek is waarschijnlijk helemaal te verklaren door mensen die geplanned zwanger worden (en ook bij de eerste keer zwanger werden).
Het alcohol-argument is wellicht iets van de laatste tijd; ik kan me dan ook goed voorstellen dat de piek kleiner wordt als je verder terugkijkt.